灾难性遗忘是指在微调过程中,模型学习新的任务时忘记了原有任务的知识,在原始任务上的表现灾难性地下降。灾难性遗忘是一个普遍存在且尚未被很好地根除的问题。本文尝试总结了几种避免灾难性遗忘的思路及方法。
参考资料:
- (1)为什么神经网络会存在灾难性遗忘(catastrophic forgetting)这个问题? - 刘斯坦的回答 - 知乎
- (2)Continual Learning 笔记: EWC / Online EWC / IS / MAS
文章列表:
- [1]Overcoming catastrophic forgetting in neural networks (EWC)
- [2]PackNet: Adding Multiple Tasks to a Single Network by Iterative Pruning
- [3]REMIND Your Neural Network to Prevent Catastrophic Forgetting
- [4]Essentially No Barriers in Neural Network Energy Landscape
- [5]Orthogonal Gradient Descent for Continual Learning
思路一、参数更新(微调时)
最直观的解决思路就是从参数更新着手。大模型的知识是存储在参数中的,大模型的遗忘直接由参数的改变导致。对原始模型的参数进行各种保护,可以有效地减缓灾难性遗忘的发生。
1. Elastic Weight Consolidation (EWC) [1]
EWC 的核心思想是在微调过程中,对原始模型的参数进行保护。具体来说,EWC 通过在原始模型的损失函数中加入正则项,对原始模型的参数进行约束。这个正则项的形式是对原始模型的每个参数 $w_i$ 计算一个 Fisher 信息矩阵 $F_i$,然后对所有参数的 Fisher 信息矩阵求和,最后乘以一个超参数 $\lambda$,作为正则项加入到原始模型的损失函数中。这个正则项的作用是约束原始模型的参数不要发生太大的变化,从而保护原始模型的知识。
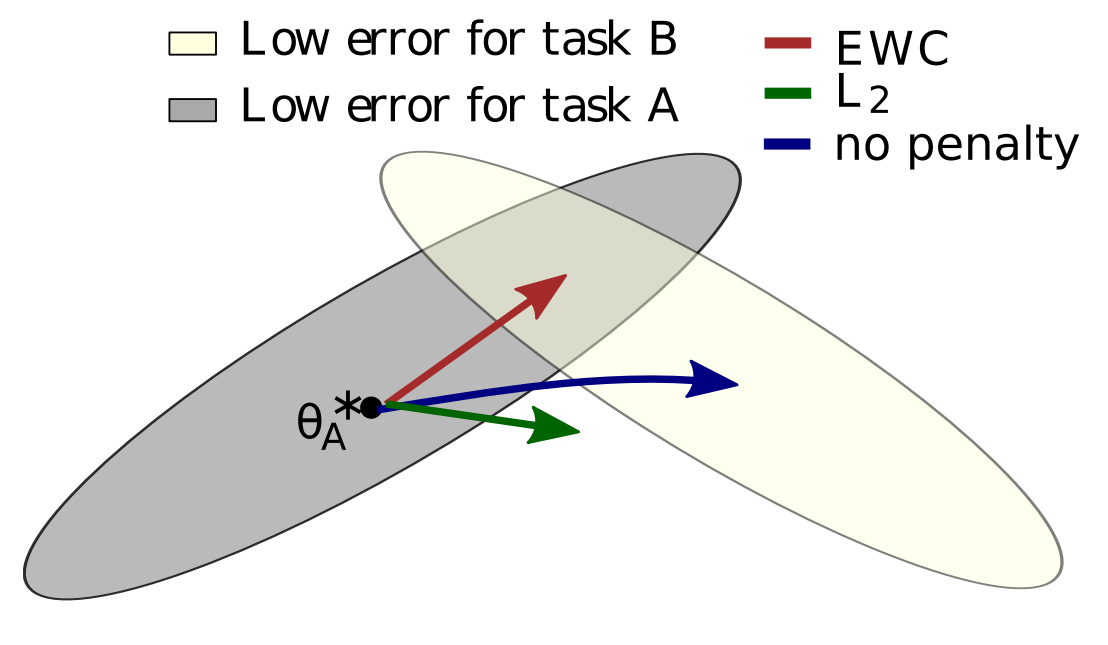
直观理解如图。图中的三个箭头代表了三种正则化策略下参数空间的变化。蓝色箭头是在没有正则化约束的微调路径。参数会直奔新任务的最优点,但是很大可能会忘记原始任务的知识。绿色箭头是在 L2 正则化约束下的微调路径,意在令微调的参数不会远离原本任务最优点太多。但直接加 L2 正则项没有考虑不同参数对任务的重要性,限制了微调的效果。
最后,红色箭头是在 EWC 约束下的微调路径。计算每个参数 $\theta_i$ 之于原始任务的重要性 $\Omega_i$, 定义正则项的损失函数为:
\[L(\theta) = L_B(\theta) + \frac{\lambda}{2} \sum_i \Omega_i (\theta_i - \theta_{A,i}^*)^2\]其中,$\theta_{A,i}^*$ 是参数 $\theta_i$ 在原始任务上的最优值。根据不同的 $\Omega_i$ 设置,可以得到不同的 regularization-based 方法。(2) 中有更详细的介绍。
2. 冻结参数
在实践中大家已经发现,对于一个大模型任务真正有用的参数只有一小部分。只要这一小部分参数不发生变化,模型的相关知识就不会丢失。基于这个想法,围绕冻结参数展开的各种方法应运而生。比如 PackNet [2], 通过网格压缩将重要参数冻结,然后在剩下的参数上训练新的任务。
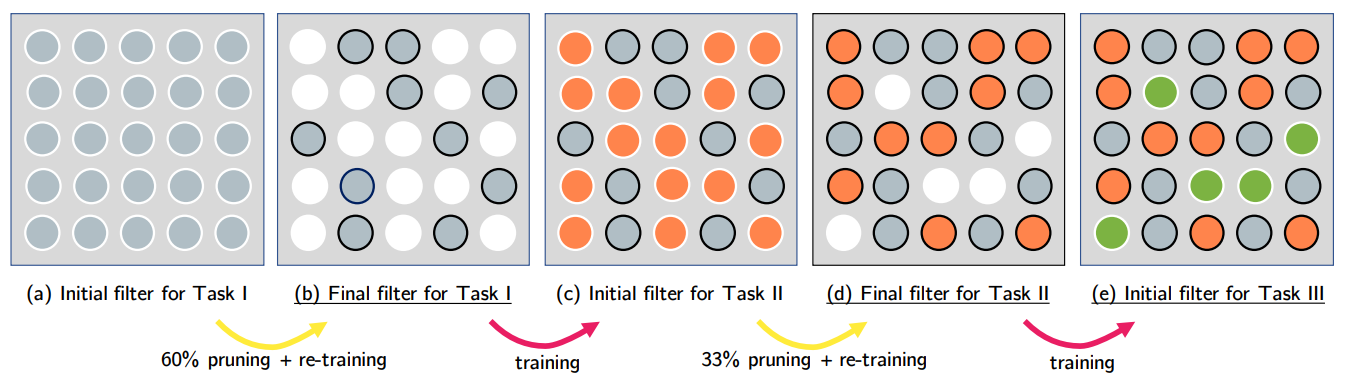
这种非常直观方法需要面对一个同样直观的问题,那便是未被冻结的参数可能不够表达新的任务。于是有许多研究尝试在训练时动态扩张网络参数以容纳新的任务空间。不过这种做法在本文的思路分类中应当属于模型结构的范畴了。
3. 复习
如果说新的训练任务不可避免地会将参数向远离原始任务最优点的方向“拉”,那么通过复习原始任务便可以再给参数一个回到原始任务最优点的“力”。此时我们便可以期待这两股力的合力能让模型沿着尽量靠近原始任务的路线更新,将模型带向一个对两种任务都还算满意的位置。
复习的方式不一而足,除了直接将原原本本的原始数据再一次喂给模型学习,还有一些简化的,或是基于关键特征等等的方式。这与人类的复习方法(划重点,复习关键笔记)有相似之处。REMIND [3] 便是一种基于特征的复习方法,其流程如图。
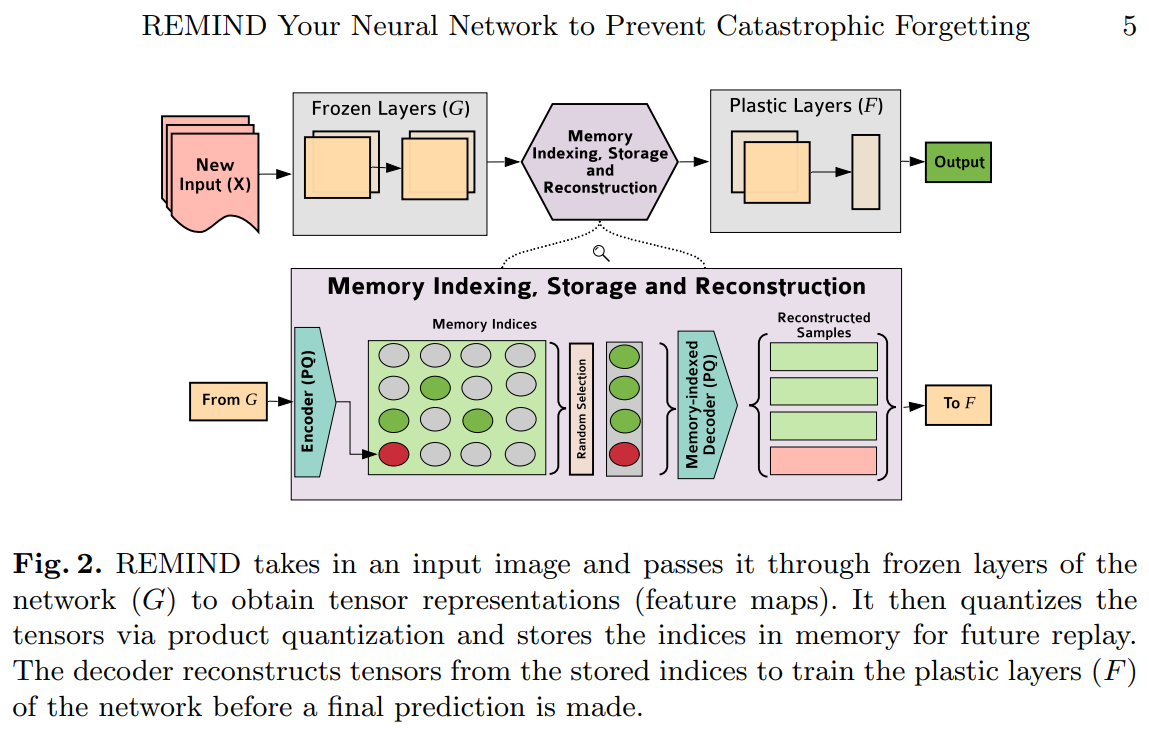
REMIND 将输入传过 Frozen Layers 和一个编码器,得到一个输入的 feature map。这个 map 在量化后被作为 Memory Indices 保存下来,供以后复习。一个解码器负责从 Memory Indices 重建出样本用以训练 Plastic Layers。
思路二、优化视角
这个思路不是我目前关心的部分,故暂时完全拷贝 (1) 中的内容。
从优化角度理解也很直观,下面是两个不同任务的损失曲面,现在假设上面那个大片片的任务训练完了,要在下面那个很多丘陵的任务上继续训练:

- 两个损失曲面示意图,蓝色箭头是当前点在原任务上的梯度,红色箭头是新任务上的梯度,蓝色轨迹为走红色路线后投影在原任务损失面上的轨迹。
然后你会发现,当前所在的点可能位于第一个任务的底部了,但却位于第二个任务的山峰上,你如果照着第二个任务的梯度(红色箭头)滑下去,第一个任务的损失越爬越高,那立马就挂了,这就是灾难性遗忘。
那么怎么克服这个问题?
找到一个平坦区域
如果位于第一个任务的平坦区域,那么即便第二个任务再野,也不会影响第一个任务,这个很好理解吧。说白了就是训练一个泛化性很好的模型,所有提高泛化性的手段都可以用上去。
找到连通路径
这篇论文 Essentially No Barriers in Neural Network Energy Landscape [4] 说了,神经网络的所有的极小值其实都是连通在一起的,文章还提出了如何从一个极小值找到一条通路连到另一个极小值的算法。
那么很容易想到,我可以从原始任务的某个极小值出发,在优化新任务的时候尽量沿着底部的通道走,就可以保证原始任务不受影响了。这个算法和EWC高度类似。
考虑高维度
还有一个思路是我们考虑到神经网络的网络层是位于超高维度的,那么在优化新任务的时候,我如果保证优化的方向和原始任务不相干就可以了。所以就出现了那篇 Orthogonal gradient descent for continual learning [5] 的论文,就是保证在优化新任务的时候产生的梯度和原始任务产生的梯度在一个低秩空间是垂直的。因为神经网络的权重维度特别高,所以实现这一点并不难。
其实你仔细想想,这和基于 Pruning 的方法又是很类似了,Pruning 直接锁住重要的权重不动,只优化不重要的,相当于是用一个极端暴力的方法保证新任务梯度和原始任务梯度垂直。因为那些被压缩掉的权重,往往得到的梯度很少。
思路三、模型结构
沿着参数更新的思路能够提出许多方法减少微调时对原始参数的改变。然而,直接保留完整的原始模型,通过追加新的结构完成模型的微调似乎更加有效——无论是从规避参数改变导致的灾难性遗忘的角度,还是从微调计算量的角度。许多 Parameter-Efficient Finetuning 都符合这个思路的设想。例如新增参数层的 Adapter-based 及 LoRA 系列,扩展每层参数的 Prefix-Tuning,基于 Prompt 的 Prompt-Tuning 和 P-Tuning 等等。因为我此前对上述方法已经有了一定的了解,故此处暂不作介绍。
并不是说通过完全保留原始参数就能完美避免灾难性遗忘了。如果新增的参数太过“强大”,那么合成出的新模型依然会被彻底带偏。然而这类高效的微调方式相比全量微调更容易控制,也更容易推倒重来。通过改换模块,还能在共用原始模型的同时适应不同下游任务。这使得我们遇见灾难性遗忘时也可以只面对新增的参数,而不是整个模型,同时重训的代价也更低,是一个实践上非常友好的思路。
现有的 Parameter-Efficient Finetuning 如何进一步避免灾难性遗忘,仍需更多调研。本文将在日后更新,此处暂告一段落。